वैज्ञानिक तारों की दूरी कैसे ज्ञात करते हैं, जरुर जानिए

Distance of Stars From Earth –  जब भी आप रात में आसमान में तारों को देखते हैं तो मन में यह सवाल तो उठता ही होगा कि आखिर यह तारा हमसे कितना दूर है। कुछ तारों की दूरी तो हमें ज्ञात है पर आज भी ब्रह्माण्ड में ऐसे कई तारे हैं जिनकी दूरी के बारे में कोई नहीं जानता। वैसे जिन तारों की हम पृथ्वी से दूरी जानते हैं उनकी दूरी वैज्ञानिक आखिर कैसे निकालते हैं आइये इस विषय पर जानते हैं –

खगोलविज्ञानी ब्रह्माण्डीय दूरी को मापने के लिए कई विभिन्न तरीकों का उपयोग करते है। खगोलीय दूरी मापने में उपयोग होनेवाली सभी विधियां विज्ञान और गणित के अद्भुत संयोजन का उदाहरण है। पर इस लेख में हम दो विधियों की चर्चा करेंगे –

• राडार मापन(Radar Measurement)
• लंबन विधि(Parallax method)

राडार मापन(Radar Measurement):

दूरी मापने का यह भी एक आधुनिक तरीका है। यह विधि इस तथ्य पर आधारित है की प्रकाश(रेडियो तरंग, माइक्रोवेव, दृश्य प्रकाश, X-किरण) 300000 km/s की रफ़्तार से यात्रा करता है। यह तकनीक सबसे सटीक मानी जाती है लेकिन इस विधि की भी अपनी सीमाएं है। खगोलविज्ञानी इस विधि से सौरमंडल तक कि दूरी तो निर्धारित कर सकते है लेकिन इससे अधिक दूरी के लिए यह विधि उपयोगी नही है। वैज्ञानिकों ने सौरमंडल में स्थित ग्रहों की दूरी निर्धारण के लिए इस तकनीक का उपयोग कई बार किया है खासकर पृथ्वी से चंद्रमा की दूरी मापने के लिए यह सबसे नियमित तरीका है।

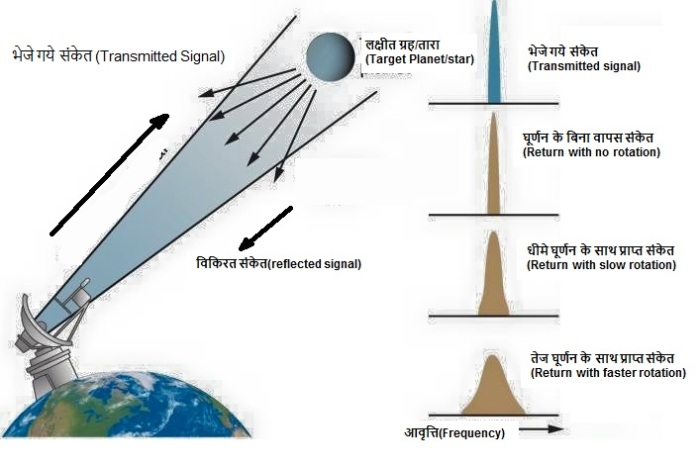
इस विधि में पृथ्वी से संचारित संकेत(Transmitted signal) उस पिंड/ग्रह पर भेजे जाते है। संकेत उस ग्रह से टकराकर वापस लौटने पर पृथ्वी के संचारित केंद्रों द्वारा पकड़ लिए जाते है। वैज्ञानिक संचारित संकेतो के जाने और लौटने में लगने वाले समय को दर्ज कर लेते है इससे उस ग्रह की दूरी का पता लगा लिया जाता है।

D(Distance) = V(Velocity) × T(Time)

यह भी जानें – अबतक का खोजा गया ब्रह्मांड का सबसे बड़ा तारा, पृथ्वी से है खरबों गुना बड़ा

लंबन विधि(Parallax method):

उपयोग करते है जिसे लंबन/तारकीय लंबन(Stellar Parallax) कहते है। दो विभिन्न बिंदुओं से किसी वस्तु की ओर देखने पर जो कोणीय विचलन(angular shift) प्रतीत होता है, उसे लंबन कहते हैं और इन बिंदुओं को मिलानेवाली आधार रेखा उस दूरस्थ वस्तु पर जो कोण बनाती है, उससे लंबन का निरूपण होता है।

सरल शब्दों में लंबन दो अलग-अलग स्थानों से देखा गया किसी तारे की स्पष्ट स्थिति में अंतर ही है जो उसके बैकग्राउंड में स्थित वस्तुओं के कारण प्रतीत होता है। आधार रेखा जितनी ही बड़ी होगी(अर्थात्‌ प्रेक्षण के बिंदु जितने ही दूर होंगे) वस्तु पर कोण उतना ही बड़ा होगा और परिणाम में सटीकता/यथार्थता की संभावना भी उतनी ही ज्यादा होगी।

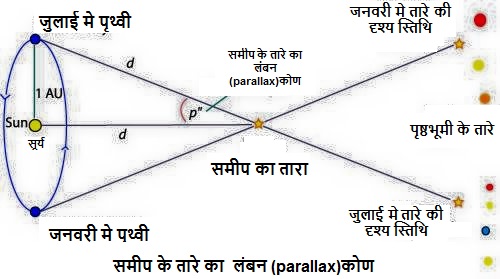
अब सवाल है लंबन विधि द्वारा बड़ी दूरियों जैसे ग्रह अथवा तारे की दूरी का मापन हम कैसे करते है ? सबसे सरल तरीका है गणितीय विधि।

किसी दूरस्थ तारे/ग्रह S की दूरी D ज्ञात करने के लिए, हम इसको पृथ्वी पर स्थित दो वेधशालाओं से भी प्रेक्षण कर सकते है लेकिन जैसा हमने ऊपर बताया की प्रेक्षण के बिंदु जितने ही ज्यादा दूर होंगे परिणाम की सटीकता उतना ही बेहतर होगी। इसलिए खगोलविज्ञानी पृथ्वी के परिक्रमण व्यास को अपनी प्रेक्षण बिंदु बनाते है इसके लिए बस खगोलविदों को 6 महीने के अंतराल पर प्रेक्षण करना पड़ता है।

मान लीजिए प्रेक्षण बिंदु A तथा B है।

A एवं B के बीच की दूरी AB = b

इन दो स्थितियों से तारे की प्रेक्षण दिशाओं AS तथा BS के बीच का कोण θ = ∠ ASB माप लिया जाता है। यह कोण लम्बन कोण या लम्बनिक कोण(parallax angle) कहलाता है।
तारे की पृथ्वी से दूरी D बहुत अधिक है अतः

b << D

इसलिए कोण θ बहुत ही छोटा है। अतः हम S को वृत्त का केंद्र, AS = D को त्रिज्या तथा AB = b चाप मान सकते हैं।

∵ त्रिज्या AS = BS,
∴ चाप AB = b
∵ कोण θ = चाप/त्रिज्या = AB/AS
θ = b/D
अतः तारे की दूरी
D = b/θ

इस सूत्र में मान रख कर लम्बन-विधि से ग्रह अथवा तारे की पृथ्वी से दूरी ज्ञात कर सकते हैं। यहाँ पर पृथ्वी के परिक्रमण व्यास को अपनी प्रेक्षण बिंदु बनाया गया है इसलिए वह दूरी 2AU(खगोलीय इकाई: Astronomical unit) है।

∴ तारे की दूरी D(Parsec) = 1/p(arcseconds).

दूरस्थ तारों का लंबन कोण बहुत ही छोटा होता है उसका मापन अर्कसेकंड(arcseconds) में किया जाता है। चूंकि तारों की दूरी भी बहुत अधिक होती है इसलिए उसका मापन भी पारसेक(Parsec) में किया जाता है। यदि किसी तारे का लंबन कोण 0.723 अर्कसेकंड है तो उस तारे की दूरी होगी
D = 1/0.723 = 1.38 पारसेक।

लंबन विधि तारो की दूरी ज्ञात करने के लिए एक अच्छी विधि है लेकिन इस विधि की भी अपनी सीमाएं है। नजदीकी तारों की दूरी ज्ञात करने में यह विधि बेहद कारगर है लेकिन बहुत ज्यादा दूरी पर स्थित तारों के लिए यह विधि उपयोगी नही है। यदि ज्ञात लंबन कोण 0.01 अर्कसेकंड से भी छोटी है तब तारो की दूरी तय करना बड़ा कठिन होता है खासकर तब जब आपका प्रेक्षण बिंदु पृथ्वी पर ही स्थित हो क्योंकि ऐसी स्थितियों में पृथ्वी का वातावरण भी बड़ा प्रभाव डाल देता है। यही वजह है की पृथ्वी पर स्थित टेलिस्कोप के मुकाबले अंतरिक्ष में स्थित टेलिस्कोप तारों की दूरी संबंधित ज्यादा अच्छे परिणाम देते है। अंतरिक्ष में स्थित टेलिस्कोप 0.001 अर्कसेकंड/लंबन कोण पर भी दूरी का सटीक आकलन करने में सक्षम है।

अभी भी आप सोच रहे होंगे की ये तो केवल 100 या 1000 पारसेक दूर स्थित तारों की दूरी ज्ञात करने की विधि है जबकि तारो की ब्रह्मांडीय दूरी तो बहुत ज्यादा है। यहां हम अन्य विधियों की भी चर्चा करेंगे जो बड़ी खगोलीय दूरी मापने में प्रयोग में लायी जाती है।

अधिक जानकारी के लिए आप ये लिंक फोलो करें – https://vigyanvishwa.in/2018/04/01/stellardistance/

दोस्तों, विज्ञानम् को स्पोर्ट कीजिए, इसे हमें मिलकर हिन्दी में विज्ञान का सबसे बड़ा पोर्टल बनना है तो आप हमें सहयोग कर सकते हैं, आप इस लिंक पर जाकर हमारे लिए लिख सकते हैं – https://vigyanam.com/submit-post/

यह भी जानें – Hubble Telescope ने ब्रह्मांड में सबसे दूरस्थ तारा खोजा, जानिए कैसा दिखता है